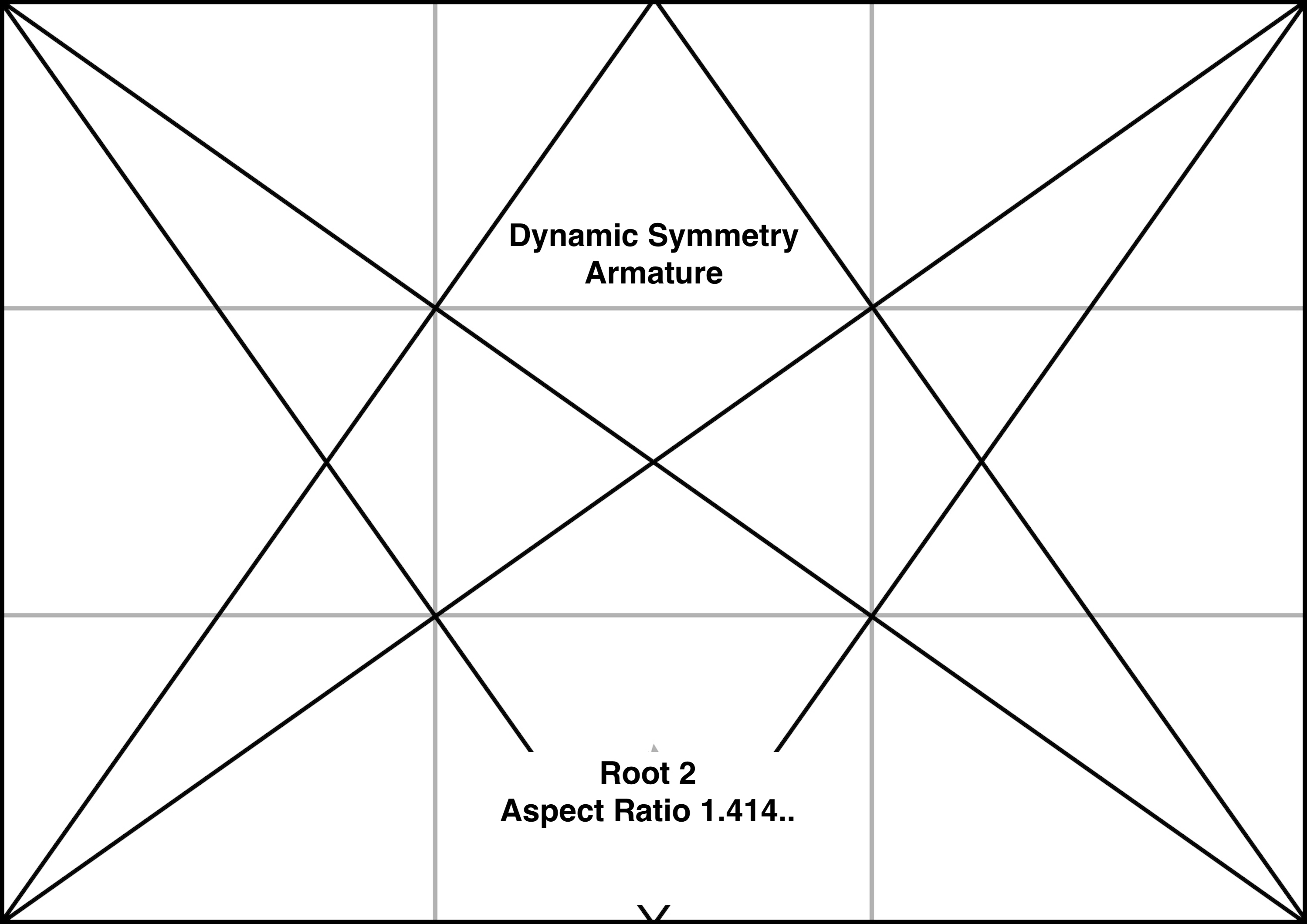
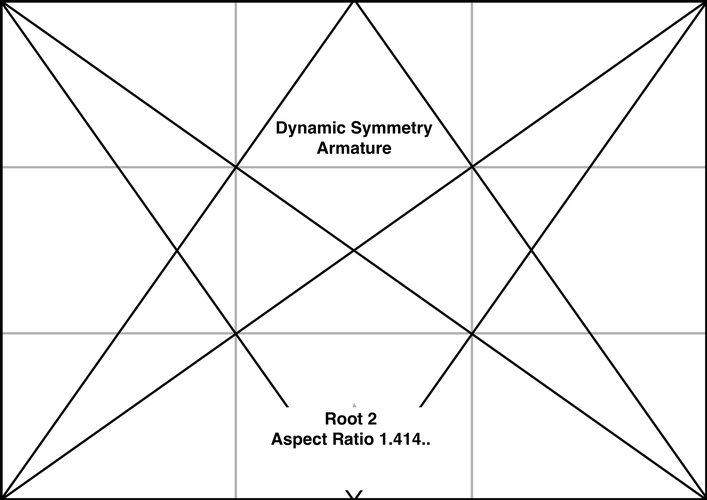
Dynamic Symmetry Armature Root 2 (1.414..)
- Material
- Oil
- Size
- Root 2 with Aspect ratio 1.414...
The vertical line dropped from the point where a reciprocal meets the top edge, marks off a vertical rectangle with the same aspect ratio as the whole rectangle (proved elsewhere by similar triangles on my blog for the general case). Just consider the right hand vertical rectangle for this discussion. Assume the large rectangle is 1xRoot 2 with the top edge of width Root 2 and the right edge of height 1 (with aspect ratio of small to large of 1 to Root 2). Let x be the distance between the upper right corner and the point on the top edge where the reciprocal meets it. Then this smaller vertical rectangle on the right has aspect ratio x:1 (smaller to larger). Since their aspect ratios are equal, we have x/1 = 1/Root 2 or x = Root 2/Root 2*Root2 = Root 2/ 2. So x = half of Root 2 or half the width of the rectangle. Root 2 is the Aspect Ratio for European A5 sizes, due to this characteristic of dividing the original rectangle in half and having the same proportions. We can fold papers in half again and again and continue to get sizes that are still in the A5 proportion. The aspect ratio of 11x14 is 14/11 = 1.2727..., close to the AR of Root PHI. Note how close this aspect ratio is to that of our common x10 or 16x20 at 1.25.
Download PDF